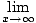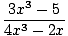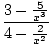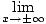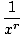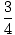Calculus way to solve asymptopes?

[Fatal Dawn]

I know calculus is used in mathematics when trying to graph the end behavior of a polynomial function. Algebra checks the end behavior.

There is no way to determine exactly where the function crosses the x axis without using calculus. All we know is the end behavior but there is no way to know how far we have to go to draw them.





When talking about rational functions is it the similar for solving asymptotes? Is there a rule in calculus that solves asymptotes?

For me I've just stuck with a 'long way' I've found of solving asymptotes algebraically. It's not the way most people use because it is longer but I've been told my way is okay.



For example:



c(t) = 4 - 3x / x + 7



I divide each term by the highest value of x. In this case I divide everything by x. I would do this if the highest quotient for an x was, for example, x^2 or x^3.



Dividing each term by x would give me 4/x - 3x/x / x/x + 7/x



For the numerator I still have 4/x but the x cancels out on -3x/x. This lets me know that -3 is the lone term.



Since (1)x/x in the denominator is the only other thing that cancels in the equation. I am left with the lone terms -3/1 or -3. The horizontal asymptote is -3.



The vertical as we know is to make the denominator equal to 0 somehow (since you can never divide any number by 0). To make that denominator 0 I would need to substitute -7 for x. Therefor the vertical asymptote is -7.



Is there a simpler way to find asymptotes that's different than this way?









Also for those wondering about the intercepts.



To find the y intercept I would have to make the equation equal to 0 by replacing every x term with a 0. 4-0/0+7 = 4/7. The y intercept is 4/7.



To find x I need to make the numerator equal to 0. 4 = -3x. x = 4/3. The x intercept is 4/3.



If we were to graph a parabola, the parabolic curve would never touch the lines designated at -7 for x and -3 for y.



On algebraic way to solve horizontal asymptote:

http://www.freemathh...asymptotes.html

 

[Evil Eye]

Is there a simpler way to find asymptotes that's different than this way?

Without using a calculator? Probably not. Then again, I don't think I've ever done this.



Expressing X in Y then using that to calculate the derivative and then calculating Y for X=0 might work... Not exactly a fast method, though

 

[Fatal Dawn]

I think what you said is probably a way of explaining what I've been doing. It's very tedious but I divide each term (denominator and numerator) by the highest quotient of x. Here's the thing, I've never understood why I've done what I've done. This is a visual example of my method.

Evaluating Limits at Infinity



In order to find horizontal asymptotes, we must evaluate limits as xapproaches infinity. To evaluate the limits of rational functions at infinity, first divide each of the terms in the numerator and the denominator by the highest. For example, to evaluate

first divide each of the terms in the numerator and denominator by the highest power of x present in the function. In this case, that is x [sup]3[/sup].

then evaluate the individual limits using the following rule: if r is a rational number greater than zero such that x [sup]r[/sup] is defined for all x , then

= 0





Applying this rule in this case leads to the following:

=

I've been told though that there was a way in calculus to find that out. The way I've seen most people use is the quick way where they look at the numbers with the highest matching x quotients in both the numerator and the denominator. So as described above it would take no time to see that 3 and 4 are the highest matching quotients so 3/4 is the asymptote.



That's why I prefer the long method because when you do the division, you will be able to notice if the numbers keep dividing onto themselves making the asymptote 0 (as anything dividing onto itself into infinity is approaching 0).



Thanks again EE.

 

[Evil Eye]

I'm not so sure what I said was correct, though

Let's see...

y=1/x

x=1/y

x'=-1/y^2

x'=0

y=-sqrt(Infinity)

Hmm, guess it works for this function. Although it's not exactly meaningful information. The other way around you can get a maximum and a minimum y for x. (At -Infinity and +Infinity, which makes sense when you think about it. The maximum just so happens to be higher than the minimum.)

 

[Fatal Dawn]

EE, have you ever messed around with the data files in LF2?

It's pretty amazing how the designers coded the game. They have the x and y axis and also a thrid z axis (Cartesian coordinate system). They use negative and positive x/y axis points to determine everything that is positioned in game. I aIso believe they also use asymptopes in place in that game as well. I'll post the coding sometime soon.

 

[Fatal Dawn]

You're right +Mr. Jazzy everything requires math in some form or another.

Most of it is just working your way up from the basics.



Here's the data code for an LF2 char:



As you can see it uses frames and mathematics to calibrate positions in the game. For one character you could have pages of these codes. Every thing - whether it be a character, object, stage, etc. uses these codes.

<bmp_begin>

name: Bandit

head: sprite\sys\bandit_f.bmp

small: sprite\sys\bandit_s.bmp

file(0-69): sprite\sys\bandit_0.bmp  w: 79  h: 79  row: 10  col: 7

file(70-139): sprite\sys\bandit_1.bmp  w: 79  h: 79  row: 10  col: 7

file(140-209): sprite\sys\bandit_0b.bmp  w: 79  h: 79  row: 10  col: 7

file(210-279): sprite\sys\bandit_1b.bmp  w: 79  h: 79  row: 10  col: 7

walking_frame_rate 3

walking_speed 4.000000

walking_speedz 2.000000

running_frame_rate 3

running_speed 8.000000

running_speedz 1.300000

heavy_walking_speed 3.000000

heavy_walking_speedz 1.500000

heavy_running_speed 5.000000

heavy_running_speedz 0.800000

jump_height -16.299999

jump_distance 8.000000

jump_distancez 3.000000

dash_height -11.000000

dash_distance 15.000000

dash_distancez 3.750000

rowing_height -2.000000

rowing_distance 5.000000

<bmp_end>



<frame> 0 standing

   pic: 0  state: 0  wait: 5  next: 1  dvx: 0  dvy: 0  dvz: 0  centerx: 39  centery: 79  hit_a: 0  hit_d: 0  hit_j: 0 hit_Fa: 235 hit_Ua: 295 hit_Da: 265 hit_Fj: 280

   bpoint:

	  x: 39  y: 35

   bpoint_end:

   wpoint:

	  kind: 1  x: 23  y: 55  weaponact: 23  attacking: 0  cover: 0  dvx: 0  dvy: 0  dvz: 0

   wpoint_end:

   bdy:

	  kind: 0  x: 21  y: 18  w: 43  h: 62

   bdy_end:

<frame_end>



<frame> 1 standing

   pic: 1  state: 0  wait: 6  next: 2  dvx: 0  dvy: 0  dvz: 0  centerx: 39  centery: 79  hit_a: 0  hit_d: 0  hit_j: 0 hit_Fa: 235 hit_Ua: 295 hit_Da: 265 hit_Fj: 280

   bpoint:

	  x: 39  y: 35

   bpoint_end:

   wpoint:

	  kind: 1  x: 23  y: 54  weaponact: 23  attacking: 0  cover: 0  dvx: 0  dvy: 0  dvz: 0

   wpoint_end:

   bdy:

	  kind: 0  x: 21  y: 18  w: 43  h: 62

   bdy_end:

<frame_end>

Codes like divx (division x?) determine the rate at which an object travels upon the x axis (horizontal). The same with divy (vertical). So say if a character wants to perform an action like jump or kick it determines how high and how far. Pretty much like slope in algebra. But here it is used for angle of trajectory.



hitDj (downwards jump) or hitFj(forward jump) determine controls. What keyboard buttons should be pressed to perform an action.



Bpoint or bloodpoint for example determines where the character bleeds (all characters bleed from the mouth so the bpoint is usually around the same). Same concept of slope. Here it is used for positioning.



I think LF2 uses a bit of both algebra and calculus concepts.

 

[Evil Eye]

EE, have you ever messed around with the data files in LF2?

I have not. I have, however, tried my hand at 3D rendering. Walking around a simple room, looking around.

Ray casting was sort of easy, still trying to get polygons to render, though.

Lots and lots of mathematics is involved... Sine and Cosine to determine movement for example.

Suppose we have a character (camera) with an X and a Y position (can't go up or down). Walking around is easy as long as you can't rotate the camera. Once you start rotating moving when pressing forward isn't as simple as increasing Y anymore.

Then there's things like the fish eye effect... it's a pain

 

[Fatal Dawn]

I've always believed that if you can code a web page, that you can code an LF2 data file. It really does run like a web program. Just looking at the structure you can see the two are quite similar. Like in web programs you have hash tags, just like html <body> and <head> tags you have these throughout (ex: the <frame> tags). LF2 is pure numbers. Ratios, slopes, coordinates, functions - all converted to numbers. For me the area in mathematics I am good at is purely numbers, I'm no good at geometry or things like that.

 

[Evil Eye]

Yeah, I noticed the tags. Looks like a form of XML to me, a simpler form maybe. Does it care about case?

 

[Fatal Dawn]

It doesn't care about case. However spaces need to be marked with underscores. Also of course you can't leave broken tags.

 

[Fatal Dawn]

Have you ever noticed that games tend to favor patterns?

This game likes to use patterns like say dividing by 1/2: It would jump from 4 to 2. And from 20 to 10. And from 10 to 5.

During the game they have objects which fall from the sky: like this http://www.freewebs.com/jayspa/lf2.gif





I was looking at the objects and how they behave in game.



You see that all these objects have the same number of frames and you wonder how could this be. How could both a boulder and a baseball have the same number of frames? But you see it is not number of frames that matters but the wait times. It's actually a brilliant way to mimic real world outside forces such as wind-resistance and weight without affecting the objects too much. So at first it really does seem that the boulder falls the same rate as the baseball, but during free-fall the baseball has longer wait time for the frames, it will seem like it is twisting and turning while the boulder is falling flat.



For something like a boomerang you'd need a much more complex idea, because here you are talking about a whole new trajectory. But for ah object like the boomerang you are not following a simple vertical trajectory, but an exponential function. Here you would still have the same constant but with 2 sets of values: one negative (e^-bx) and one positive (e^bx).

 

[Evil Eye]

Is that image supposed to move?

Have you ever noticed that games tend to favor patterns?

So does Newtonian physics, it'd look wrong otherwise. Besides, it's easier

Fewer frames also means a smaller and faster game. Could be important.

 

[Fatal Dawn]

Is that image supposed to move?

No it's a still image of Henry's Sonata of Death move. Without a doubt, probably the most interesting move of the game - Henry (the guy in brown) plays his flute which leaves any and everything around him suspended in mid-air. [media]http://www.youtube.com/watch?v=1de3CsnzrZ8[/media]



It's probably the most difficult move in the game to code:

<frame> 252 flute

pic: 141 state: 3 wait: 9 next: 253 dvx: 0 dvy: 0 dvz: 0 centerx: 36 centery: 79 hit_a: 0 hit_d: 999 hit_j: 0

sound: data\057.wav

wpoint:

kind: 1 x: 39 y: 48 weaponact: 30 attacking: 0 cover: 1 dvx: 0 dvy: 0 dvz: 0

wpoint_end:

itr:

kind: 10 x: -34 y: -71 w: 142 h: 220 vrest: 1 injury: 1 zwidth: 76

itr_end:

itr:

kind: 10 x: -97 y: -58 w: 258 h: 207 vrest: 1 injury: 1 zwidth: 55

itr_end:

itr:

kind: 10 x: -126 y: -40 w: 318 h: 189 vrest: 1 injury: 1 zwidth: 34

itr_end:

itr:

kind: 11 x: -184 y: -37 w: 438 h: 200 vrest: 1 injury: 1 zwidth: 76

itr_end:

bdy:

kind: 0 x: 22 y: 8 w: 36 h: 73

bdy_end:

<frame_end>

Each frame is like this one which requires several kinds of itr (interaction). Firstly vrest is an important code word for being able to hit many different enemies, unlike most attacks which are arest and hit only single enemies. There are roughly 34 vrests for this specific move - each with a value of 1 - this basically means that there is virtually no escape (for 34 seconds). This one attack is actually a series of attacks and - for 34 seconds - you have roughly 1 second to escape.



w (width) and h (height) determine how far-reaching the attack is. Most attacks don't reach the hundreds just to give you an idea of how devastating this attack is.

So does Newtonian physics, it'd look wrong otherwise. Besides, it's easier

Fewer frames also means a smaller and faster game. Could be important.

Certainly, it makes things a lot easier to create patterns. You'd think with a simple game like this that it'd have less frames, but that's quite the opposite. There are sheets and sheets of frames. That's what I love about this game, it is simple yet dynamic in so many aspects. There are limitless amounts of ingenious combos and tactics to come up with, and they give the computer high AI. You never get bored playing it.

 

[Evil Eye]

Certainly, it makes things a lot easier to create patterns. You'd think with a simple game like this that it'd have less frames, but that's quite the opposite. There are sheets and sheets of frames.

Oh, I dunno, sprites are a lot easier than full 3D. Sprites only have to be drawn, 3D animations have to be calculated. (Trust me, it's a pain

)

Looks like a pretty cool game, by the way.