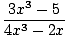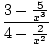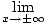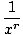I know calculus is used in mathematics when trying to graph the end behavior of a polynomial function. Algebra checks the end behavior.
There is no way to determine exactly where the function crosses the x axis without using calculus. All we know is the end behavior but there is no way to know how far we have to go to draw them.
When talking about rational functions is it the similar for solving asymptotes? Is there a rule in calculus that solves asymptotes?
For me I've just stuck with a 'long way' I've found of solving asymptotes algebraically. It's not the way most people use because it is longer but I've been told my way is okay.
For example:
c(t) = 4 - 3x / x + 7
I divide each term by the highest value of x. In this case I divide everything by x. I would do this if the highest quotient for an x was, for example, x^2 or x^3.
Dividing each term by x would give me 4/x - 3x/x / x/x + 7/x
For the numerator I still have 4/x but the x cancels out on -3x/x. This lets me know that -3 is the lone term.
Since (1)x/x in the denominator is the only other thing that cancels in the equation. I am left with the lone terms -3/1 or -3. The horizontal asymptote is -3.
The vertical as we know is to make the denominator equal to 0 somehow (since you can never divide any number by 0). To make that denominator 0 I would need to substitute -7 for x. Therefor the vertical asymptote is -7.
Is there a simpler way to find asymptotes that's different than this way?
Also for those wondering about the intercepts.
To find the y intercept I would have to make the equation equal to 0 by replacing every x term with a 0. 4-0/0+7 = 4/7. The y intercept is 4/7.
To find x I need to make the numerator equal to 0. 4 = -3x. x = 4/3. The x intercept is 4/3.
If we were to graph a parabola, the parabolic curve would never touch the lines designated at -7 for x and -3 for y.
On algebraic way to solve horizontal asymptote:
http://www.freemathh...asymptotes.html
There is no way to determine exactly where the function crosses the x axis without using calculus. All we know is the end behavior but there is no way to know how far we have to go to draw them.
When talking about rational functions is it the similar for solving asymptotes? Is there a rule in calculus that solves asymptotes?
For me I've just stuck with a 'long way' I've found of solving asymptotes algebraically. It's not the way most people use because it is longer but I've been told my way is okay.
For example:
c(t) = 4 - 3x / x + 7
I divide each term by the highest value of x. In this case I divide everything by x. I would do this if the highest quotient for an x was, for example, x^2 or x^3.
Dividing each term by x would give me 4/x - 3x/x / x/x + 7/x
For the numerator I still have 4/x but the x cancels out on -3x/x. This lets me know that -3 is the lone term.
Since (1)x/x in the denominator is the only other thing that cancels in the equation. I am left with the lone terms -3/1 or -3. The horizontal asymptote is -3.
The vertical as we know is to make the denominator equal to 0 somehow (since you can never divide any number by 0). To make that denominator 0 I would need to substitute -7 for x. Therefor the vertical asymptote is -7.
Is there a simpler way to find asymptotes that's different than this way?
Also for those wondering about the intercepts.
To find the y intercept I would have to make the equation equal to 0 by replacing every x term with a 0. 4-0/0+7 = 4/7. The y intercept is 4/7.
To find x I need to make the numerator equal to 0. 4 = -3x. x = 4/3. The x intercept is 4/3.
If we were to graph a parabola, the parabolic curve would never touch the lines designated at -7 for x and -3 for y.
On algebraic way to solve horizontal asymptote:
http://www.freemathh...asymptotes.html